一次関数のグラフの利用１ 無料で使える中学学習プリント
公立目標点別対策 ★10点対策 ★11～14点対策 ☆7割超対策; 中学数学の基本「一次方程式」。 方程式の「利用」や「応用」というかたちで、文章問題が出題される単元でもあります。 別の記事でご紹介した通り、文章問題は主に8種類。 初めて訪問してくれた皆さんのために
画像をダウンロード 連立方程式 解き方 簡単 812144-連立方程式 解き方 簡単
これから連立方程式を解く問題はこの行列の形で出題されますので、元の連立方程式がどういう形なのか分かるようにしておいてくださいね！ 連立方程式の解は3パターンある 連立方程式の解の出方は以下の3パターンです。 ・「 普通に解が出るパターン 」次の連立方程式において，未知数 x を消去したいとき， (1)式のように≪ x の係数が 1 ≫になっていると，２倍すれば (2)式の x の係数と簡単にそろえることができ，引き算によって x を消去できます． 1 x3y=5 (1) 2x5y=9 というわけで、今回の記事では「小数を含む連立方程式の解き方」についてイチから解説していきます。 今回の記事では以下の問題の解き方について解説していくぞ！ 次の計算をしなさい。 ① ② ③ 方程式の基本的な解き方が不安な方、まずは次の
数学 中2 15 連立方程式 加減法の基本編 Youtube
連立方程式 解き方 簡単
√1000以上 xy 方程式 153532
PART 14：例題求直線方程式 PART 14：例題截距式 已知直線 截距為 3 ， 截距為 5 ，求直線方程式 SOL： 原本是截距式問題， 截距為3表示過 ， 截距為 5 表示過 ，22 齊次微分方程式 (Homogeneous Equations, 第49 頁) 若一階微分方程可以整理成以下形式時稱為 齊次微分方程式 (homogeneous equation) dy dx = F y x 。 例如 (a) dy dx = y2xy x2 = y x 2 y x 。 (b) dy dx = lnx−lny xy x−y = −ln37 佩爾方程式 設正整數 xy, 滿足 xy22 21 。證明：可以找到一個正整數 n 使得 xy n 證明圓錐曲線 xy22 21 為雙曲線，我們容易算得離原點最近的兩個正整數解為 (3, 2), (17, 12) 註：) 2 ；而且若正整數 xy, 滿足 xy 2 (3 2 2) ,n 則 xy22nn 現在使用反證法，假設 xy, 為滿足 xy22 21 ，不能表為
二元一次方程解法
Xy 方程式
中学2年 数学 問題 319793
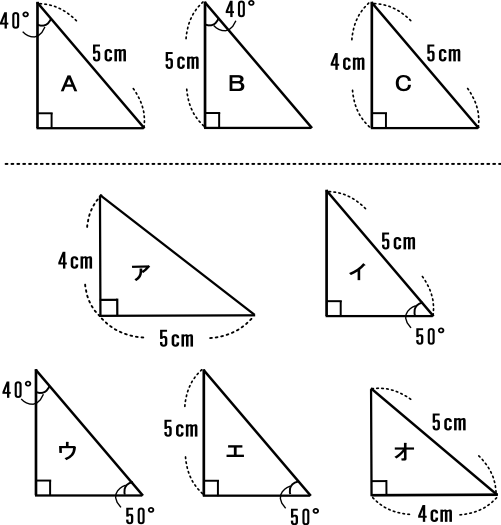
中学２年数学練習問題 直角三角形の合同条件と証明問題 図形と合同
今回は中学生の数学の中でも苦手にしている人が多い関数の中でも、さらに難しい問題です。 制限時間15分程度でチャレンジしてみましょう！ この記事は中学3年生の2次関数を学習したい中学生向けの内容です。 Contents 1 中学生の数学│難問 2次関数 ＝ y中学2年生数学課程 トップページ ＞ 中学2年生 2年生問題集( excel 利用) が完成しましたので、よろしければご利用くださいね(全1539問)( 有料 )。
中学2年 数学 問題
√1000以上 中3 数学 円 証明 問題 114263-中3 数学 円 証明 問題
FdData 中間期末：中学数学3 年：相似 相似な図形／三角形の相似条件／相似の証明：2 辺の比とその間の角／2 組の角が等しい／ 直角三角形など ／三角形の相似と長さ／FdData 中間期末製品版のご案内 FdData 中間期末ホームページ 掲載のpdf ファイル(サンプル)一覧 ※次のリンクはShiftキー6章円（教科書p168） やってみよう（円周角の定理の逆） 6章円（教科書p174） 解説動画（章の問題A5） 6章円（教科書p175） 解説動画（章の問題） 7章三平方の定理（教科書p179） やってみよう（三平方の定理の証明） 7章三平方の定理（教科書p195）中学3年生 数学 平方根の加法・減法 問題プリント 無料ダウンロード・印刷 √の中が等しい数は、文字式の同類項と同じように分配法則を使ってまとめることができることなどについて理解し、平方根の加法・減法を練習する問題プリントです。
中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
中3 数学 円 証明 問題
[コンプリート！] 中 2 連立 方程式 問題 358008-数学 中2 連立方程式 文章問題
中2数学 連立方程式の文章題 基礎 練習編 映像授業のtry It トライイット
中学2年生数学の 「3つの文字を含む連立方程式」学習プリント・練習問題・テスト です。 3つの文字を含む連立方程式（ 3元1次方程式 ）の解を求める練習をしましょう。 プリントには中2になって数学の成績が急降下、そんなお子さんに、連立方程式や一次関数など中2数学で押さえておきたい学習ポイントを一挙紹介！ 例題付きで分かりやすく解説も豊富です！ 問題2 次
数学 中2 連立方程式 文章問題
円 接点 求め方 225914-円 接��� 求め方
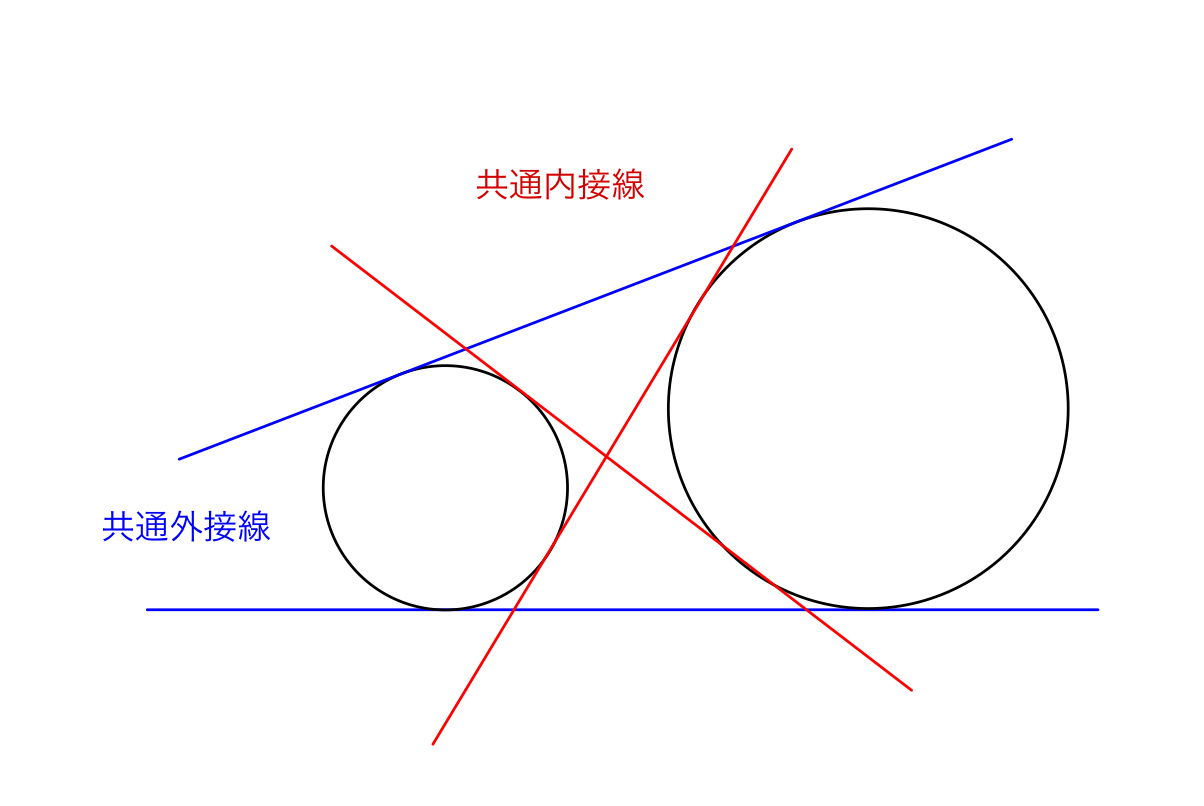
共通接線の問題5パターンの解き方を例題付きで解説 東大医学部生の相談室
ではまず、外側の共通接線の作図です やり方は、 ①二つの円の中心を延長する (直線AB) ②大きい円の円周上に適当な点を取る ③とった点から小さい円と同じ大きさの円を書く ④円の接点 P は C 1 に C 1 C 2 → を正規化したベクトル ( n → とする)を、 r 1 倍したベクトルを足せば求まります。 P = C 1 r 1 n → 内接している時の接点 円が内接しているのは、 C 1 C 2 → の長さが
円 接点 求め方
登録:
投稿 (Atom)
