共通接線の問題5パターンの解き方を例題付きで解説 東大医学部生の相談室
ではまず、外側の共通接線の作図です やり方は、 ①二つの円の中心を延長する (直線AB) ②大きい円の円周上に適当な点を取る ③とった点から小さい円と同じ大きさの円を書く ④円の接点 P は C 1 に C 1 C 2 → を正規化したベクトル ( n → とする)を、 r 1 倍したベクトルを足せば求まります。 P = C 1 r 1 n → 内接している時の接点 円が内接しているのは、 C 1 C 2 → の長さが
円 接点 求め方
円 接点 求め方- 二つの円の接線の求め方 2つの円の接線を作図する方法を以下に示します。 二つの円と距離を定義 2つの円の半径をr、r'中心間の距離をlと定義します。 r o r o' l 接線との平行線を作図 指定した3点を通る円の式 作者 SeaGull さん 本ライブラリは会員の方が作成した作品です。 内容について当サイトは一切関知しません。

点a A B を通り円x Y R に接する直線の方程式の求め方 数学ii By ふぇるまー マナペディア
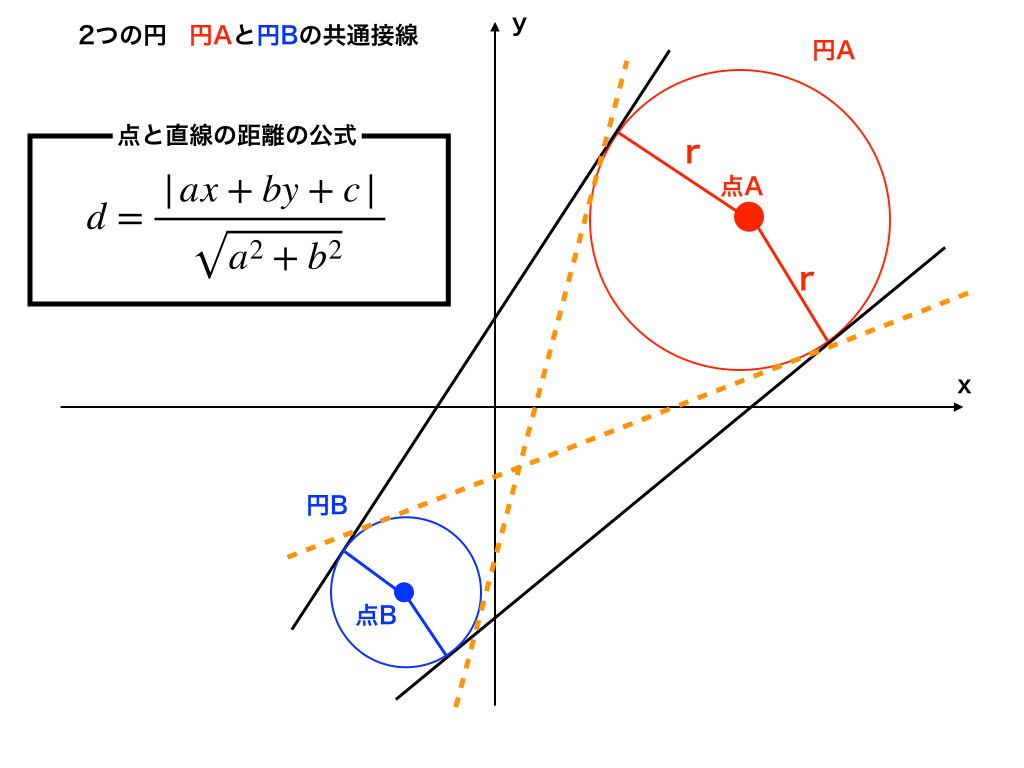
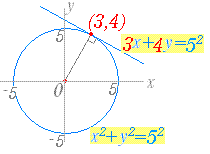
まずは、接線の方程式を数式にしないといけません。 というわけで、以下を使います。 円の中心が原点でない場合の接線の方程式の与え方の1つになります。 (公式)非原点中心の 2交点を通る直線や曲線の式 (図形と方程式3) <この記事の内容>:円と円の交点を通る『直線や曲線・円の式』が、 (kは実数で文字は何でも構いません)で表すことができる"理由"円と直線の交点を求めましょう。 円は中心座標(xc,yc)とその半径(R)で表現できます。 直線は2点(始点と終点)の座標(x、y)で表現できます。 始点座標は(xs, ys)、 終点座標は(xe,ye)とします
点と直線の距離の公式を利用 一つ目の円で接点を\(\small{ \ (x_1, \ y_1) \ }\)とおいて公式から導いた接線の方程式がもう一つの円に接することを点と直線の距離の公式を使って求めよHatena これまで円の接線の求め方を学習してきました。 今回は、円の接線の求め方を整理してみましょう。 接線の接線の求め方には 円の中心と弦が作る三角形の面積の最大 円周上の点における接線の方程式 x₁xy₁y=r² とその証明 円外の点から引いた接線の方程式 円と放物線の位置関係 2つの円の位置関係、直交する2
円 接点 求め方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ | 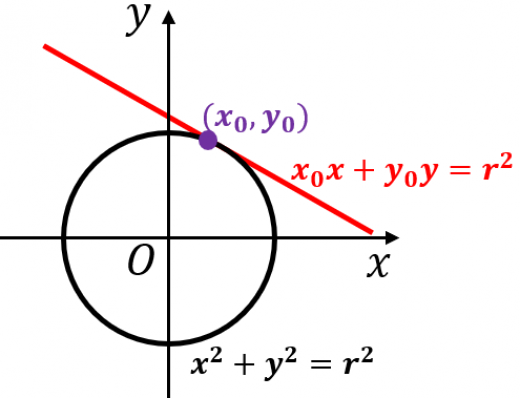 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ | 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ | 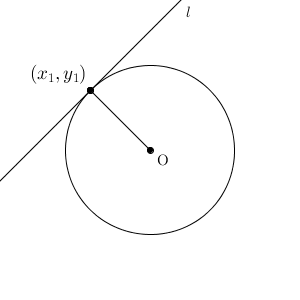 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ | 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ | 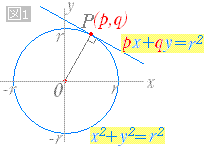 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ | 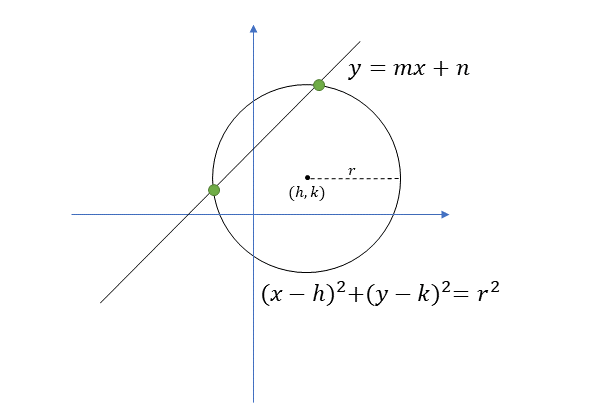 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ | 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ | 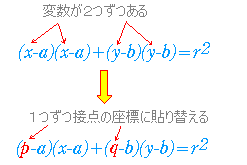 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ | 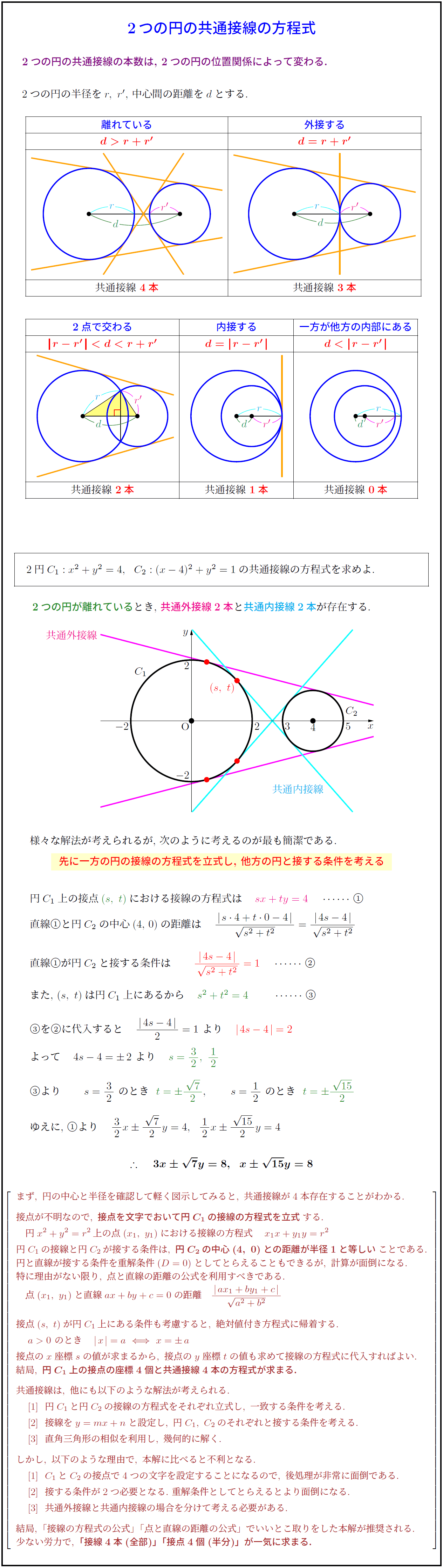 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ | 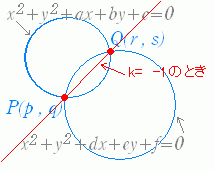 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ | 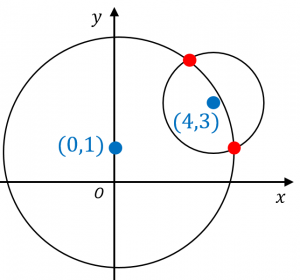 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ | 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ | 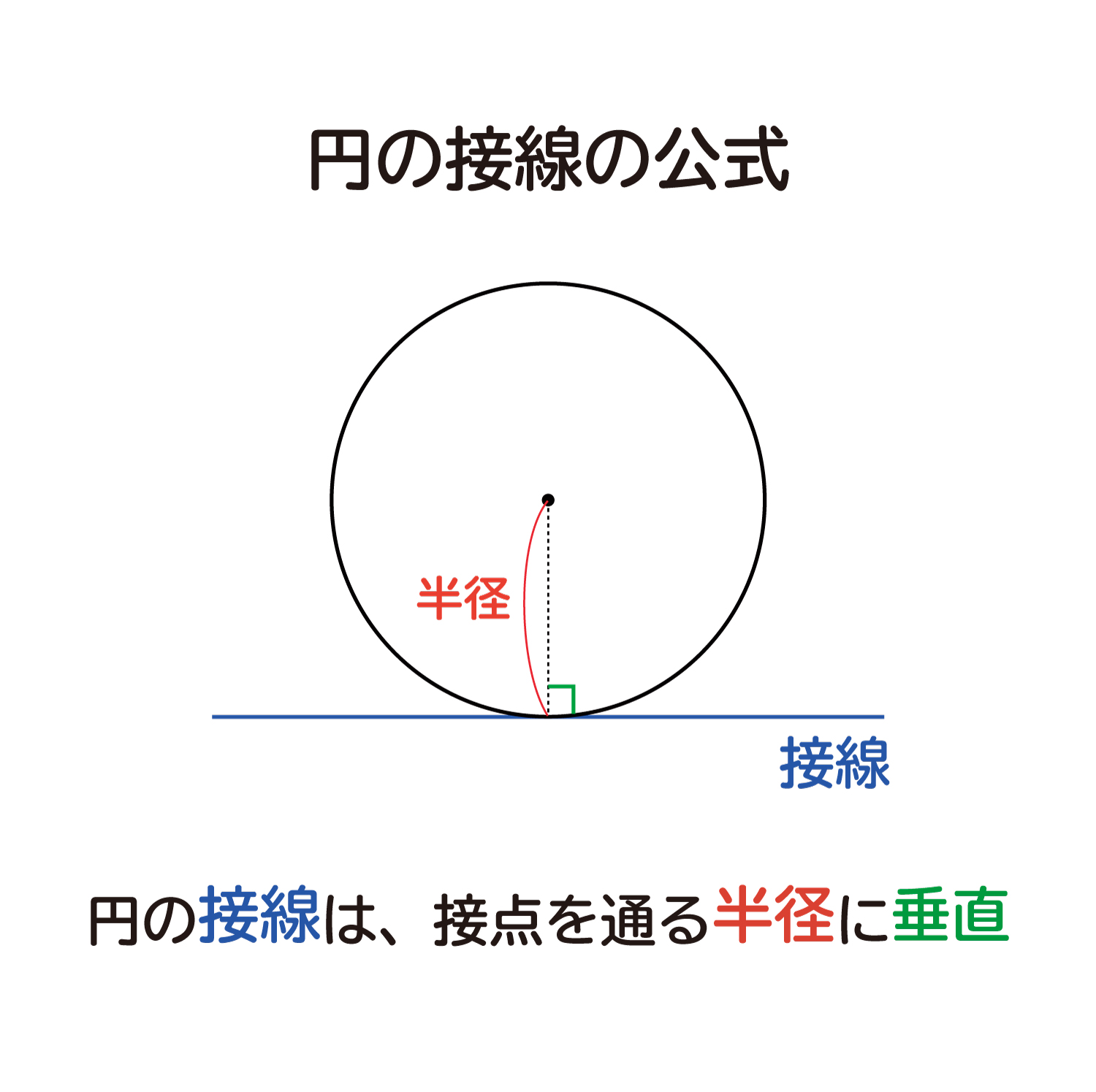 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ | 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ | 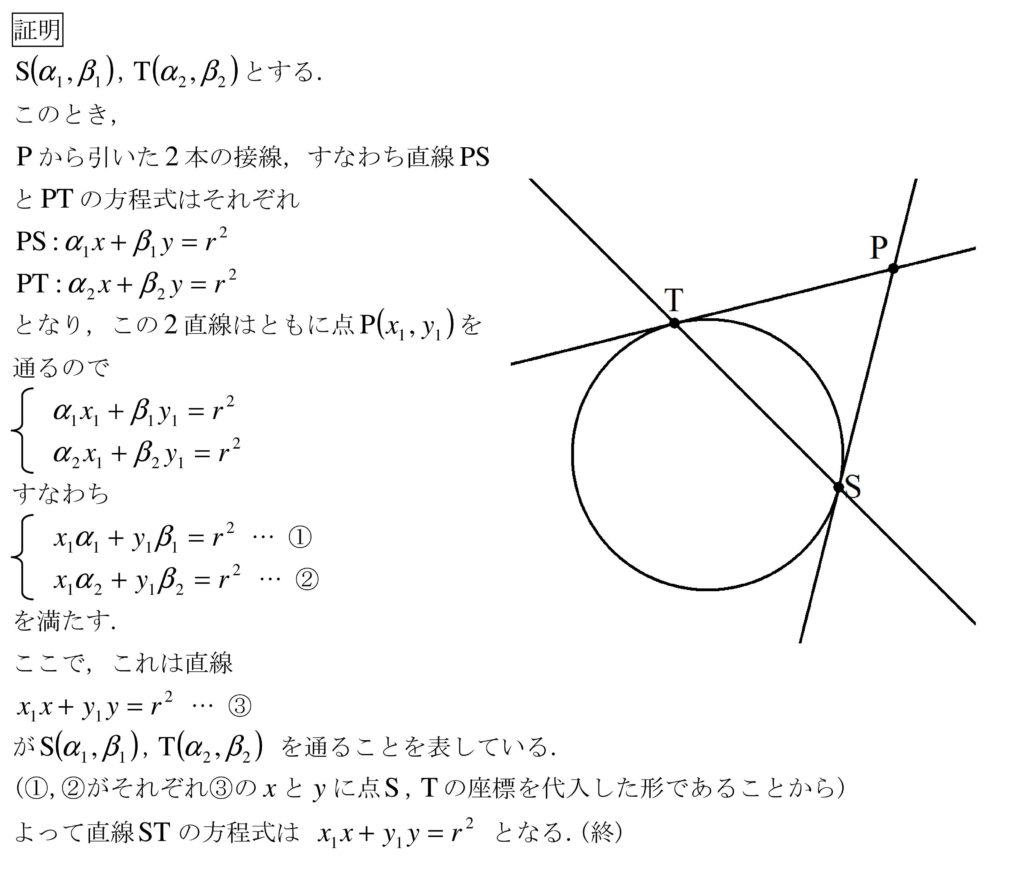 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ | 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ | 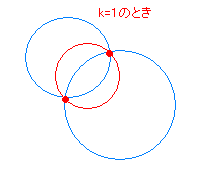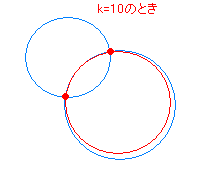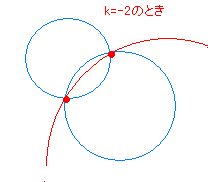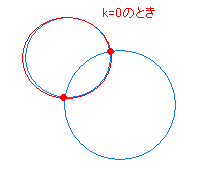 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ | 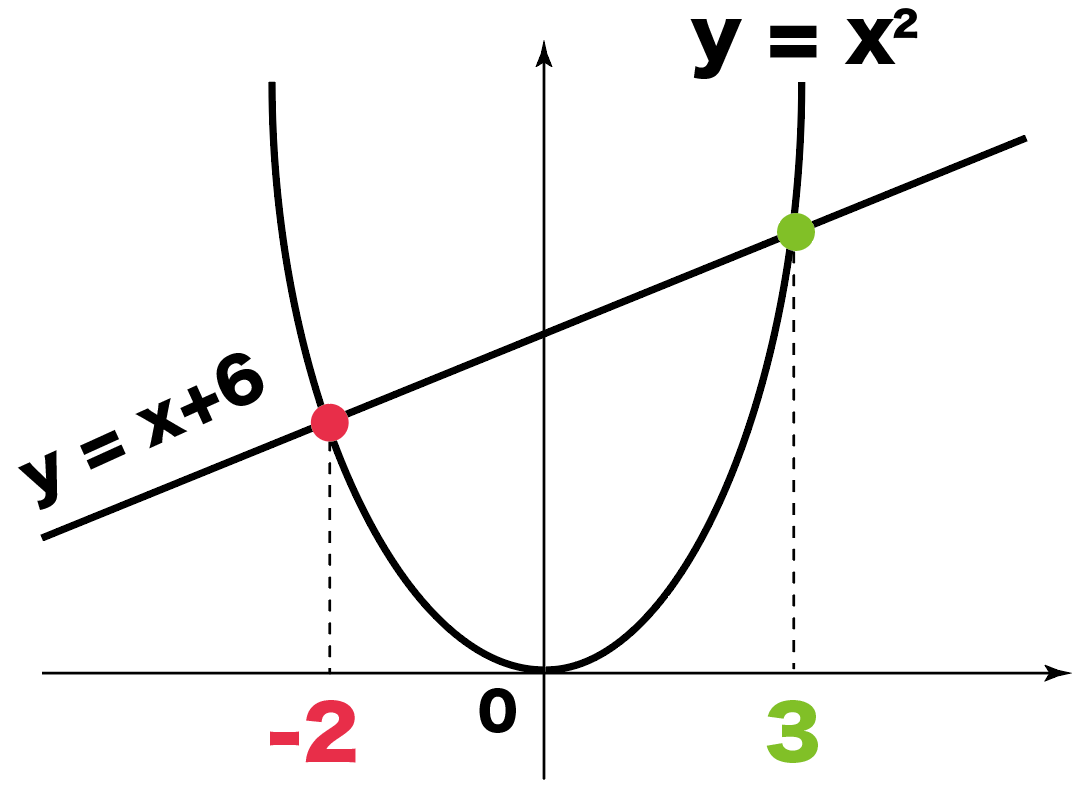 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ | 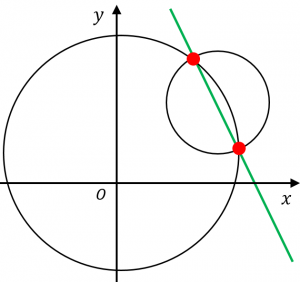 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ | 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ | 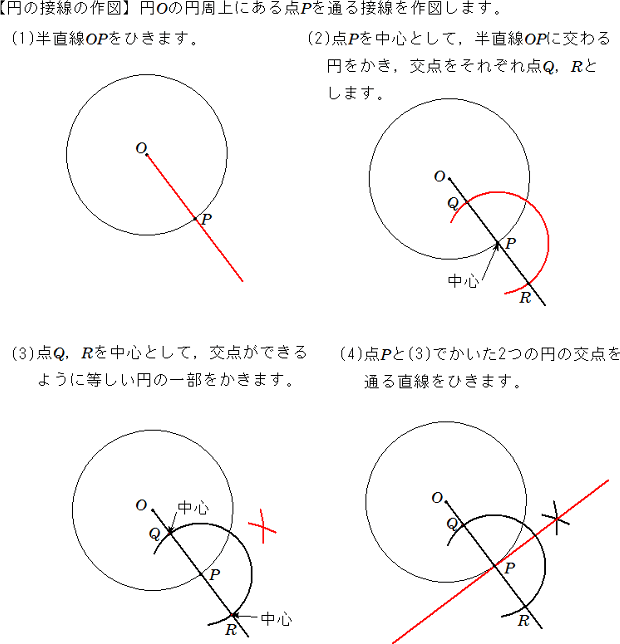 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ | 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |  円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ | 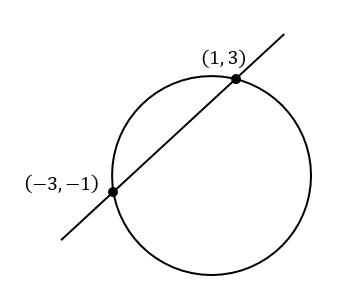 円と円の交点 座標の求め方 計算のやり方をイチから解説 数スタ |
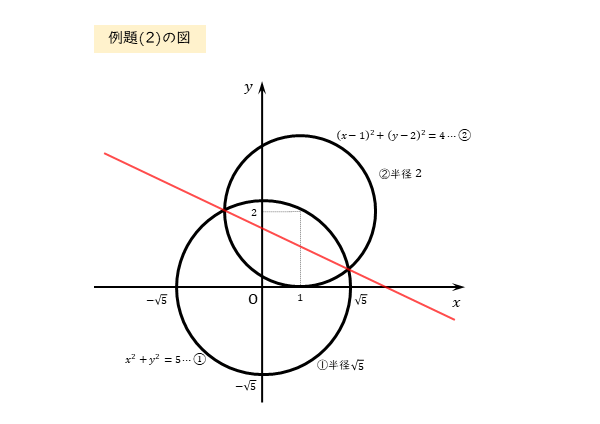
円と放物線の共有点(交点)の求め方 例えば x2y2 = 1 x 2 y 2 = 1 と y=x2 y = x 2 の交点を求めるとき、この円と放物線の式を連立したらいいよね。 {x2y2 = 1 y =x2 { x 2 y 2円と円の交点を求めてみます。 どちらの円も任意の位置にあると面倒なので、片方の円は原点中心とします。 上の円の方程式から、下の円の方程式を引きます。 ここで、 とおけば、 と直線の方程
Incoming Term: 円 接点 求め方,




0 件のコメント:
コメントを投稿