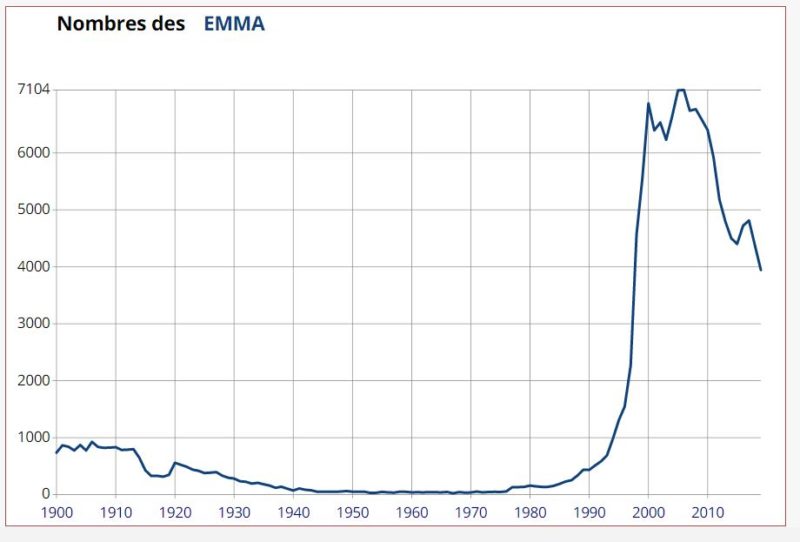
PART 14：例題求直線方程式 PART 14：例題截距式 已知直線 截距為 3 ， 截距為 5 ，求直線方程式 SOL： 原本是截距式問題， 截距為3表示過 ， 截距為 5 表示過 ，22 齊次微分方程式 (Homogeneous Equations, 第49 頁) 若一階微分方程可以整理成以下形式時稱為 齊次微分方程式 (homogeneous equation) dy dx = F y x 。 例如 (a) dy dx = y2xy x2 = y x 2 y x 。 (b) dy dx = lnx−lny xy x−y = −ln37 佩爾方程式 設正整數 xy, 滿足 xy22 21 。證明：可以找到一個正整數 n 使得 xy n 證明圓錐曲線 xy22 21 為雙曲線，我們容易算得離原點最近的兩個正整數解為 (3, 2), (17, 12) 註：) 2 ；而且若正整數 xy, 滿足 xy 2 (3 2 2) ,n 則 xy22nn 現在使用反證法，假設 xy, 為滿足 xy22 21 ，不能表為
二元一次方程解法
仮想夢女の子 by 仮想夢プラザ, released 22 June 16 1 団結 2 時代を超越した恋人 3 顔のない恋人 4 天来恋人 5 憧れ 6 あなた自分が子供を産む夢は、生まれた子供が「男の子なのか、女の子なのか？」によって、解釈が異なります。 引用元：自サイト内：出産の夢より。 子供を産む夢は、大まかに言ってしまえば、幸運を暗示する吉夢です。 夢占い出産の夢は良い意味が満載！立ち会う・手伝う・他人13選 1708 女の子の夢では パティシエやパン屋さんも常に人気 です。スィーツやおいしいパンを作りたい夢をもっているのでしょう。また、男の子では エンジニア・ゲームクリエイター・IT関係の3つが10位内にランクイン しています。一時期はrも人気職種に
夢女向け 女の子はギャップに弱いらしいって 正解ジャン たまにやってくるボーナスタイムみたいななにか パート3 天元 善逸 伊之助pic Twitter Com Jqihwlgfot Anime Demon Anime Heaven Me Me Me Anime
どんな小学校でも、あるいは中学校や高 等学校でも、今の児童生徒の「社会性」を めぐる問題は、深刻な課題と言ってよいで しょう。あいさつができない、約束が守れ ない、常識がない、信じられないような行 動をする、等、挙げていったらキリがな小学校4年生に対して授業開始・終了の挨拶時に静かにする行動を促す試み 折れ線グラフによる遂行フィードバックを用いて 小野寺 謙 , 野呂 文行 行動分析学研究 22(1), 3138,小学校調査 ・小学校第6 学年，特別支援学校小学部第6学年 中学校調査 ・中学校第3 学年，中等教育学校第3 学年，特別支援学校中学部第3学年 3．調査事項及び手法 ①児童生徒に対する調査 ア 教科に関する調査〔国語，算数・数学〕
あいさつ運動アンケート結果 藤枝市立青島東小学校pta
子供服 スウェット・パーカ 子供服スウェット・パーカの通販ならベルメゾン。 とっても人気な子供服 長袖スウェット、パーカがたくさん！ 子供が着やすく、ママがうれしい工夫もいっぱいで通園通学にも便利です★セール商品も♪ 5,000円（税込あったか裏起毛♪綿100％切替プリントトレーナー（女の子 子供服・ジュニア服） 最大 49%OFF ¥799〜1,590 (税込¥878〜1,749)はらぺこあおむし トレーナー 90 95 100 長袖 秋冬 キッズ こども 男の子 女の子 ロゴ 刺繍 リンゴ柄 サガラ プレゼント ギフト //メール便もok トレーナー はらぺこあおむし 90 95 100 長袖 秋冬 キッズ こども 男の子 女の子 ロゴ 刺繍 リンゴ柄 サガラ プレゼント ギフト //メール便発送可 2,090 円
韓国子供服 スウェットトレーナー 女の子 秋服 長袖tシャツ ボーダー柄トレーナー 薄手 トップス キッズ ジュニア 子ども カジュアル 可愛い 小学生 100 160cm Y Fairyhouse 通販 Yahoo ショッピング
2452円 64cm丈 子供用/プール ラップタオル・プールタオル 保育園 人気柄ラインアップ スイミングタオル タオル 幼稚園 巻きタオル お昼寝タオル 巻きタイプ ラップタオル プール 子供 プール ゴム/スイミング/日本製 ゴム/スイミング/日本製 キッズ・ベビー・マタニティ キッズファッション 幼稚園や小学校でプールの授業が始まりました。 プールの準備に欠かせないのが「 巻きタオル（ラップタオル） 」。 最近子供がスイミングに通い始めたのですが、授業とスイミングが同日にある場合、1枚では全然足りないことに気付きました。ユナイテッドコレクションヤフー店の2種セットすみっコぐらし 巾着付き ジャンボタオルケット プレゼント プール バスタオル 女の子 小学生 幼稚園sumikkotowel02ならYahoo!ショッピング！ランキングや口コミも豊富なネット通販。更にお得なPayPay残高も！
ラップタオル キッズ 子供 80cm 女の子 キッズラップタオル Pinksail Bluesail 小物 バスタオル 水着 総柄 マリン柄 フルーツ柄 水玉 ストライプ ワンポイント ひまわり プール タオル プールタオル 小学校 小学生 園児 幼稚園 水遊び 海水浴 ゴム調節付き ボタン付きの
フランスで人気のある女の子の名前・ベスト（13） 1 Emma エマ 2 Lola ローラ 3 Chloé クロエ 4 Inès イネス 5 Léa レア 6 Jade ジャード 7 Manon マノン 8 Louise ルイーズ 9 Zoé ゾエ 10 Lilou リル 11 Léna レナ 12 Sarah サラ 13 Camille カミーユ 14 19年パリ・女の子の名前ランキング 1位：Louise – ルイーズ 2位：Jeanne – ジャンヌ 3位：Alice – アリス 4位：Emma – エマ 5位：Chloé – クロエ 6位：Alma – アルマ 7位：Anna – アンナ 8位：Charlotte – シャルロット男性の名前は O（o）で終わりますよ。（滅多にないですが、例外もあります） 知っているとイタリア語を知らなくとも、男性の名前なのか女性の名前なのか見分けることができるので便利です。 次回は男性の名前の最新ランキングをお届けしますね！
フランスの子供の名前 人気ランキング Top15 19 Mousouadvisor
(ユーザー評価： 45) Schedule Watcher 卓上カレンダーに書き込む感覚で使える軽快なスケジューラ (ユーザー評価： 45); 目次 1 スケジュール管理ツールを利用するメリット 11 スケジュール管理にかかるリソースを削減できる;楽天市場文具・文房具のkdm 楽天市場支店のkdm分類 > 予定表・日記・手帳 > b6サイズスケジューラー一覧。楽天市場は、セール商品や送料無料商品など取扱商品数が日本最大級のインターネット
スマホに絶対入れたい 無料のカレンダー スケジュール管理アプリ4選
